Compartilhe :
O conceito de plano foi introduzido pelos matemáticos da antiguidade que representavam um plano como um ente primitivo geométrico infinito a duas dimensões.
A Equação vetorial paramétrica do plano é expressa por:
1) Escreva caso possível a equação geral do plano α que passa em:
A = (1,1,1)
B = (3,-6,2)
C = (2,5,-1)
Resolução
Montando os vetores
$\overrightarrow{AB}=\left( B-A \right)=\left( 3,-6,2 \right)-\left( 1,1,1 \right)=\left( 2,-7,1 \right)$
$\overrightarrow{AC}=\left( C-A \right)=\left( 2,5,-1 \right)-\left( 1,1,1 \right)=\left( 1,4,-2 \right)$
$\overrightarrow{Ax}=\left( x-A \right)=\left( x,y,z \right)-\left( 1,1,1 \right)=\left( x-1,y-1,z-1 \right)$
Aplicando a regra de Sarrus
$\left( 14.\left( x-1 \right)+1.\left( y-1 \right)+8.\left( z-1 \right) \right)-\left( -4\left( y-1 \right)+4\left( x-1 \right)-7\left( z-1 \right) \right)=0\Rightarrow $
$\left( 10.\left( x-1 \right)+5.\left( y-1 \right)+15.\left( z-1 \right) \right)=0\Rightarrow $
$=10x-10+5y-5+15z-15=0\Rightarrow 10x+5y+15z=30\Rightarrow $
Dividindo por 5
$2x+y+3z=6$
2) Escreva a equação do plano que tem os pontos A = (1,1,-1), B = (2,2,0), e C = (0,6,2)
Resolução
Montando os vetores
$\overrightarrow{AB}=\left( B-A \right)=\left( 2,2,0 \right)-\left( 1,1,-1 \right)=\left( 1,1,1 \right)$
$\overrightarrow{AC}=\left( C-A \right)=\left( 0,6,2 \right)-\left( 1,1,-1 \right)=\left( -1,5,3 \right)$
$\overrightarrow{Ax}=\left( x-A \right)=\left( x,y,z \right)-\left( 1,1,-1 \right)=\left( x-1,y-1,z+1 \right)$
Aplicando a regra de Sarrus
$\left( 3.\left( x-1 \right)-1.\left( y-1 \right)+5.\left( z+1 \right) \right)-\left( 3\left( y-1 \right)+5\left( x-1 \right)-1\left( z+1 \right) \right)=0\Rightarrow $
$\left( -2.\left( x-1 \right)-4.\left( y-1 \right)+6.\left( z+1 \right) \right)=0\Rightarrow -2x+2-4y+4+6z+6=0\Rightarrow $
$\Rightarrow -2x-4y+6z=-12$
Dividindo por -2
$x+2y-3z=6$
 |
| Retrato do filósofo e matemático Euclides de Alexandria |
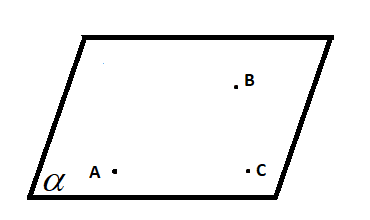
O filosofo e matemático Euclides de Alexandria disse que por três pontos distintos e não alinhados, passa um e somente um plano, logo para definir a equação vetorial paramétrica da plano consideremos figura abaixo e vamos chamar esse plano de α.
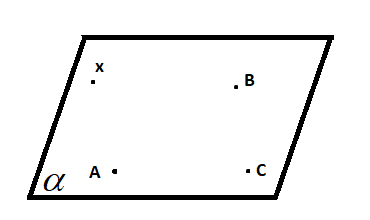
Esse plano α apresenta infinitos outros planos e digamos que um deles é x, logo poderemos afirmar que os vetores x-A, B-A, e C-A estão contidos no mesmo plano.
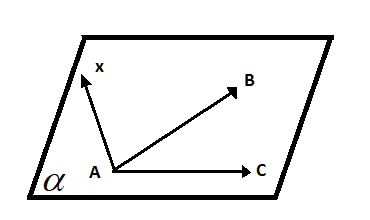
Sendo esses vetores coplanares, logo um desses vetores pode ser expresso em função dos outros dois.
A Equação vetorial paramétrica do plano é expressa por:
Exemplos de exercícios resolvidos
1) Escreva caso possível a equação geral do plano α que passa em:
A = (1,1,1)
B = (3,-6,2)
C = (2,5,-1)
Resolução
Montando os vetores
$\overrightarrow{AB}=\left( B-A \right)=\left( 3,-6,2 \right)-\left( 1,1,1 \right)=\left( 2,-7,1 \right)$
$\overrightarrow{AC}=\left( C-A \right)=\left( 2,5,-1 \right)-\left( 1,1,1 \right)=\left( 1,4,-2 \right)$
$\overrightarrow{Ax}=\left( x-A \right)=\left( x,y,z \right)-\left( 1,1,1 \right)=\left( x-1,y-1,z-1 \right)$
Aplicando a regra de Sarrus
$\left( 14.\left( x-1 \right)+1.\left( y-1 \right)+8.\left( z-1 \right) \right)-\left( -4\left( y-1 \right)+4\left( x-1 \right)-7\left( z-1 \right) \right)=0\Rightarrow $
$\left( 10.\left( x-1 \right)+5.\left( y-1 \right)+15.\left( z-1 \right) \right)=0\Rightarrow $
$=10x-10+5y-5+15z-15=0\Rightarrow 10x+5y+15z=30\Rightarrow $
Dividindo por 5
$2x+y+3z=6$
2) Escreva a equação do plano que tem os pontos A = (1,1,-1), B = (2,2,0), e C = (0,6,2)
Resolução
Montando os vetores
$\overrightarrow{AB}=\left( B-A \right)=\left( 2,2,0 \right)-\left( 1,1,-1 \right)=\left( 1,1,1 \right)$
$\overrightarrow{AC}=\left( C-A \right)=\left( 0,6,2 \right)-\left( 1,1,-1 \right)=\left( -1,5,3 \right)$
$\overrightarrow{Ax}=\left( x-A \right)=\left( x,y,z \right)-\left( 1,1,-1 \right)=\left( x-1,y-1,z+1 \right)$
$\left( 3.\left( x-1 \right)-1.\left( y-1 \right)+5.\left( z+1 \right) \right)-\left( 3\left( y-1 \right)+5\left( x-1 \right)-1\left( z+1 \right) \right)=0\Rightarrow $
$\left( -2.\left( x-1 \right)-4.\left( y-1 \right)+6.\left( z+1 \right) \right)=0\Rightarrow -2x+2-4y+4+6z+6=0\Rightarrow $
$\Rightarrow -2x-4y+6z=-12$
Dividindo por -2
$x+2y-3z=6$
Referências
- Notas de Geometria Analítica e Álgebra linear, Pedro Coelho, Santos, São Paulo, 2011.
- Notas de aula de Geometria Analítica e Álgebra linear, Sergio R. Lara, Santos, São Paulo, 2010.
Sobre o autor
Olá meu nome é Pedro Coelho, eu sou engenheiro químico com Pós Graduação em Engenharia de Segurança do Trabalho e também sou Green Belt em Lean
Six Sigma. Além disso, eu estou estudando Engenharia Civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)
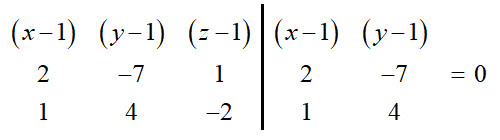
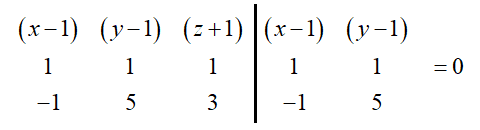
0 Comentários de "Equação vetorial paramétrica do plano: Exercícios Resolvidos"
Os comentários são sempre bem vindos, pois agregam valor ao artigo. Porém, existem algumas regras na Política de Comentários, que devem ser seguidas para o seu comentário não ser excluído:
- Os comentários devem estar relacionados ao assunto do artigo.
- Jamais faça um comentário com linguagem ofensiva ou de baixo calão, que deprecie o artigo exposto ou que ofenda o autor ou algum leitor do blog.
- Não coloque links de sites ou blogs no corpo do texto do comentário. Para isso, assine com seu Nome/URL ou OpenID.
-Não coloque seu email e nem seu telefone no corpo do texto do comentário. Use o nosso formulário de contato.
- Se encontrar algum pequeno erro na postagem, por favor, seja bem claro no comentário, pois a minha bola de cristal não é muito boa.
- Tem vezes que eu demoro pra responder, mas quase sempre eu respondo.
- Não seja tímido, se você tem alguma duvida ou sabe de algo mais sobre o assunto abordado no artigo, comente e compartilhe conosco :)