Desenvolvido por Gabriel Cramer em 1750, a regra de Cramer é uma fórmula que é usada para resolver um sistema de equações lineares contendo tantas equações quanto incógnitas, eficiente sempre que o sistema de equações tiver uma única solução.
Essa fórmula é geralmente usada para obter a solução para o sistema de equações dado formado por meio de matrizes. A solução obtida usando a regra de Cramer será em termos dos determinantes da matriz de coeficientes e das matrizes obtidas substituindo uma coluna pelo vetor coluna dos lados direitos das equações.
Definição da Regra de Cramer
A regra de Cramer é um importante método que é usado para resolver um sistema de equações. Neste método, os valores das variáveis do sistema devem ser calculados usando os determinantes das matrizes. Assim, a regra de Cramer também é conhecida como método dos determinantes.
A fórmula dessa regra considera um sistema de equações lineares com n variáveis x₁, x₂, x₃, …, xₙ escritas na forma matricial AX = B.
- A = Matriz de coeficientes (deve ser uma matriz quadrada)
- X = Matriz de colunas com variáveis
- B = Matriz coluna com as constantes (que estão no lado direito das equações)
D = |A|, Dx1, Dx2, Dx3,…, Dxn
O Dxi para i = 1, 2, 3,…, n é o mesmo determinante que D, tal que a coluna é substituída por B.
Por isso,
x1 = Dx1/D; x2 = Dx2/D; x3 = Dx3/D; ….; xn = Dxn/D {onde D não é igual a 0}
A seguir você vai dar uma olhada nas fórmulas da regra de Cramer para matrizes 2×2 e 3×3.
Regra de Cramer 2×2
A regra de Cramer para a matriz 2×2 é aplicada para resolver o sistema de equações em duas variáveis.
Consideremos duas equações lineares em duas variáveis.
a1x + b1y = c1
a2x + b2y = c2
Escrevendo essas duas equações na forma de AX = B.
Sendo:
Logo:
x = Dx/D
y = Dy/D
Exemplo de Exercício aplicando Regra de Cramer – 2×2
1 ) Resolva o seguinte sistema de equações usando a regra de Cramer:
2x – y = 5
x + y = 4
Resolução:
Escrevendo as equações na forma AX = B.
x + y = 21
4x + 2y = 66
Resolução:
Escrevendo as equações na forma AX = B.
Sendo:
Logo:
x = Dx/D = -24/-2 = 12
y = Dy/D = -18/-2 = 9
Regra de Crammer 3×3
Para encontrar a fórmula da regra de Cramer para uma matriz 3×3, precisamos considerar o sistema de 3 equações com três variáveis.
Considerando:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
Escrevendo as equações na forma AX = B.
Sendo:
Logo:
x = Dx/D, y = Dy/D, z = Dz/D; D ≠ 0
1)Resolva o seguinte sistema de equações usando a regra de Cramer:
Calculando os determinantes aplicando regra de sarrus:
Logo:
x = Dx/D = 9/9 = 1
y = Dy/D = 18/9 = 2
z = Dz/D = 27/9 = 3
2) Determine o conjunto solução do sistema
x + 2y +z = 6
2x +y -4z = 3
x + y + z =5
Escrevendo essas equações na forma AX = B.
x = Dx/D, y = Dy/D, z = Dz/D; D ≠ 0
Exemplos de Exercícios aplicando Regra de Cramer – 3×3
1)Resolva o seguinte sistema de equações usando a regra de Cramer:
x + y + z =6
y + 3z = 11
x – 2y + z = 0
Resolução:
Escrevendo essas equações na forma AX = B.
y + 3z = 11
x – 2y + z = 0
Resolução:
Escrevendo essas equações na forma AX = B.
Logo:
x = Dx/D = 9/9 = 1
y = Dy/D = 18/9 = 2
z = Dz/D = 27/9 = 3
2) Determine o conjunto solução do sistema
x + 2y +z = 6
2x +y -4z = 3
x + y + z =5
Escrevendo essas equações na forma AX = B.
x = Dx/D = -18/-6 = 3
y = Dy/D = -6/-6 = 1
z = Dz/D = -6/-6 = 1
y = Dy/D = -6/-6 = 1
z = Dz/D = -6/-6 = 1
Condições da Regra de Cramer
Existem certas condições para aplicar a regra de Cramer para resolver o sistema de equações dado. Alguns deles incluem o seguinte:
- A regra de Cramer não funciona para o sistema de equações em que D = 0, pois para encontrar os valores das incógnitas, D deve estar no denominador e, portanto, esses valores ficam indefinidos. Além disso, quando D = 0, haverá duas possibilidades para as quais o sistema pode não ter solução.
- O sistema pode ter um número infinito de soluções, logo podemos dizer que pelo menos um dos determinantes do numerador é 0 (o que significa infinitas soluções) ou nenhum dos determinantes do numerador é 0 (o que significa que não há solução).
- Se D ≠ 0, dizemos que o sistema AX = B tem uma única solução, logo a regra de Cramer nos ajuda a determinar se o sistema dado tem “nenhuma solução” ou “número infinito de soluções”, usando os determinantes que calculamos para aplicar a regra.
Referências
- https://byjus.com/maths/cramers-rule/ (acessado em 12/05/2022 as 08:11)
- Notas de Cálculo Numérico, Pedro Coelho, Santos, São Paulo, 2011.
- Notas de Tópicos de Mátematica, Me. Adilson Simões, São Paulo,2022.
Sobre o autor
 Olá meu nome é Pedro Coelho, eu sou engenheiro químico com Pós Graduação em Engenharia de Segurança do Trabalho e também sou Green Belt em Lean
Six Sigma. Além disso, eu conclui recentemente o curso de Engenharia Civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)
Olá meu nome é Pedro Coelho, eu sou engenheiro químico com Pós Graduação em Engenharia de Segurança do Trabalho e também sou Green Belt em Lean
Six Sigma. Além disso, eu conclui recentemente o curso de Engenharia Civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)




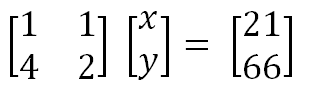








2 Comentários de "Regra de Cramer 2×2 e 3x3: Exercícios Resolvidos"
Na escola estou estudando sobre a regra de Cramer. Mas não entendi o motivo de na questão 2 da de 3×3 na DY dar (-6) sendo que minha professora disse que quando tem números iguais com sinais diferente a pessoa cortaria (não existiria mais aquele valor)
Olá anônimo
Esse seu pequeno problema está me parecendo ser uma pequena dúvida referente a regra de sinais em uma multiplicação.
Primeiramente, nós não devemos nos esquecer que quando dois números com o mesmo sinal (ambos positivos ou ambos negativos) são multiplicados ou divididos, o resultado é sempre positivo. Exemplo: (+2) × (+3) = +6.
Já quando dois números com sinais diferentes são multiplicados ou divididos, o resultado é sempre negativo. Exemplo: (-2) × (+3) = -6.
Espero ter sido claro
Um abraço
Os comentários são sempre bem vindos, pois agregam valor ao artigo. Porém, existem algumas regras na Política de Comentários, que devem ser seguidas para o seu comentário não ser excluído:
- Os comentários devem estar relacionados ao assunto do artigo.
- Jamais faça um comentário com linguagem ofensiva ou de baixo calão, que deprecie o artigo exposto ou que ofenda o autor ou algum leitor do blog.
- Não coloque links de sites ou blogs no corpo do texto do comentário. Para isso, assine com seu Nome/URL ou OpenID.
-Não coloque seu email e nem seu telefone no corpo do texto do comentário. Use o nosso formulário de contato.
- Se encontrar algum pequeno erro na postagem, por favor, seja bem claro no comentário, pois a minha bola de cristal não é muito boa.
- Tem vezes que eu demoro pra responder, mas quase sempre eu respondo.
- Não seja tímido, se você tem alguma duvida ou sabe de algo mais sobre o assunto abordado no artigo, comente e compartilhe conosco :)