Áreas de figuras planas: Exercícios resolvidos

POR Pedro Coelho

Publicado: quarta-feira, 1 de junho de 2022

Compartilhe :

 Uma figura plana é qualquer figura que possui duas dimensões, sendo que elas podem ser classificadas como regulares, no caso de existir uma lógica na sua forma, ou irregulares, no caso dessa lógica não existir.

O cálculo de áreas dessas figuras é frequente no dia a dia de diversos profissionais, seja para dimensionar o formato de uma embalagem, seja para dimensionar as áreas específicas de um novo parque fabril ou na definição das quantidades de matérias na construção civil.

Área de algumas figuras planas

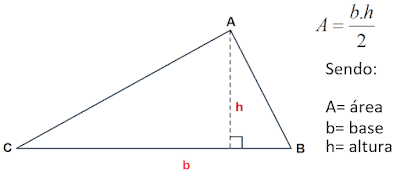
Área do triângulo

O triângulo é uma figura plana que possui três lados em três ângulos.

Sendo a sua área dada por:

Três pontos não colineares podem definir os vértices de um triângulo e a forma mais clássica de definir sua área é a partir das medidas de sua base e altura.

Caso a informação da altura do triângulo não esteja disponível, a área pode ser calculada a partir da fórmula de Heron:

$A=\sqrt{p.\left( p-a \right).\left( p-b \right).\left( p-c \right)}$

Sendo: p o semiperímetro do triângulo e a, b e c representam as medidas dos três lados do triângulo. Usando a formula de Heron, o semiperímetro do triângulo é obtido apartir da seguinte formula:

$p=\frac{a+b+c}{2}$

Outra forma para se determinar a área de um triângulo é:

$A=\frac{a.~~b.~~sen\left( \alpha \right)}{2}$

Em triângulos retângulos o método de cálculo de área mais conhecido é o Teorema de Pitágoras.

${{\left( hipotenusa \right)}^{2}}={{\left( cat.oposto \right)}^{2}}+{{\left( cat.adjacente \right)}^{2}}$

Área do quadrado

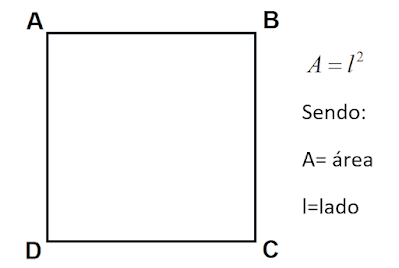
A área de uma Figura plana que possui quatro lados iguais e quatro ângulos retos é dada por:

Área do retângulo

A área de um retângulo é obtida por meio da multiplicação da base pela altura.

Área do paralelogramo

A forma de calcular a área do paralelogramo (figura que não possui todos os lados iguais nem ângulos retos) é igual ao cálculo da área do retângulo, logo:

Área do losango

Para calcular a área do losango, se usa os comprimentos de suas diagonais, logo multiplicamos a diagonal menor (d) pela diagonal maior (D), e depois se divide a área por 2, logo:

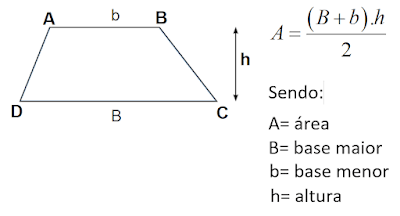
Área do trapézio

A área do trapézio é a soma das bases vezes a altura dividido por dois.

Área do circulo 

A área de um círculo é π vezes o raio elevado ao quadrado.

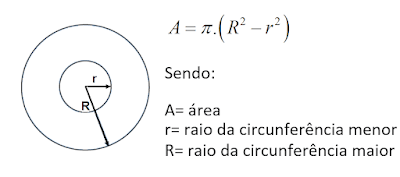
Área da coroa circular

A coroa circular é uma figura plana delimitada entre dois círculos de raios diferentes.

Área do setor circular

A área do setor circular é a área da região de um círculo delimitada por um ângulo central 𝛼.

Exemplos de exercícios resolvidos

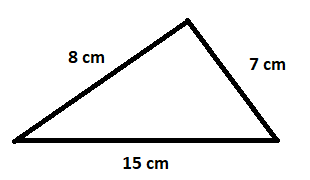
1) Calcule a área do triângulo a seguir:

Cálculo do semiperímetro

$p=\frac{8+7+15}{2}=15cm$

Cálculo da área

$A=p.\sqrt{\left( p-a \right).\left( p-b \right).\left( p-c \right)}=15.\sqrt{\left( 15-8 \right).\left( 15-7 \right).\left( 15-15 \right)}\Rightarrow $

$\Rightarrow 15.\sqrt{\left( 7 \right).\left( 8 \right).\left( 0 \right)}\cong 112,25$

2) Calcule a área do trapézio isósceles da figura, cujas medidas estão em metros.

Resolução:

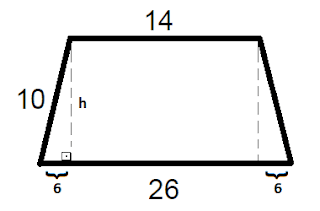
Cálculo da altura h

${{\left( hipot \right)}^{2}}={{\left( cat.op \right)}^{2}}+{{\left( cat.adj \right)}^{2}}\Rightarrow {{10}^{2}}={{6}^{2}}+{{h}^{2}}\Rightarrow $

$\Rightarrow 100=36+{{h}^{2}}\Rightarrow h=\sqrt{64}=8$

Calculo da área do trapézio

$A=\frac{\left( B+b \right).h}{2}=\frac{\left( 26+14 \right).8}{2}=160{{m}^{2}}$

Referências

• Giovanni J,R;Bonjorno, J,R; Giovanni Jr,J,R;Matemática Fundamental Uma Nova Abordagem, editora FTD, 2002.
• Notas de Tópicos de Mátematica, Me. Adilson Simões, São Paulo, 2022

Sobre o autor

Olá meu nome é Pedro Coelho, eu sou engenheiro químico com Pós Graduação em Engenharia de Segurança do Trabalho e também sou Green Belt em Lean Six Sigma. Além disso, eu estou estudando Engenharia Civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)