Compartilhe :
A função do 2º grau (também conhecida como função quadrática) é uma sentença de forma F: ℝ→ℝ, em que 𝑓(𝑥) = 𝑎𝑥²+ 𝑏x + c com 𝑎, b,c∈ℝ e 𝑎≠0 .
Como por Exemplo:
1) y = 2x² - 3x +4
2) y = -3x² +5x
3) y = x² - 7
4) y = -x²
O gráfico de uma função de 2° grau resulta em uma curva denominada parábola no plano cartesiano, sendo que a função 𝑓(𝑥) = 𝑎𝑥²+ 𝑏𝑥+ 𝑐 tem seus pares ordenados (𝑥, 𝑦) que são obtidos pela relação 𝑦= 𝑎𝑥²+ 𝑏𝑥+ 𝑐.
A parabola de um grafico de uma função de 2° grau tem a concavidade voltada para cima quando a > 0 e quando é a < 0 tem a sua concavidade virada para baixo.
x= 0 → y =a.(0²) + b(0) + c (0,c)
A parabola corta o x no ponto onde y =0
y = 0→ ax² +bx + c =0
Se o Δ for :
Δ >0 duas raizes reais e diferentes
Δ =0 duas raizes reais e iguais
Δ <0 não tem raiz real
Formula dos vertices:
Exemplos de Exercícios
Calcule a discriminante.determine quantas e quais são as raizes reais , determine as coordenadas do vertice e faça uma tabela com 5 pontos e construa o grafico das seguintes funções do 2° grau
a) y = x² - 4x +3
c) y =x²+4x +5
Resolução:
d)y = 9-x²
Referências
- Notas de Cálculo Integral e Diferencial, Pedro Coelho, Santos, São Paulo, 2010.
- Notas de Tópicos de Mátematica, Me. Adilson Simões, São Paulo, 2022.
Sobre o autor
Olá meu nome é Pedro Coelho, eu sou engenheiro químico, engenheiro de segurança do trabalho e Green Belt em Lean
Six Sigma. Além disso, também sou estudante de engenharia civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)
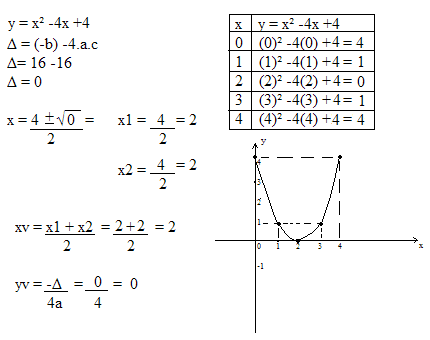
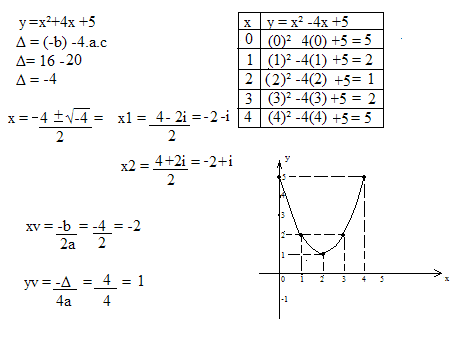
0 Comentários de "Função do 2º grau (função quadrática): Exercicios Resolvidos"
Os comentários são sempre bem vindos, pois agregam valor ao artigo. Porém, existem algumas regras na Política de Comentários, que devem ser seguidas para o seu comentário não ser excluído:
- Os comentários devem estar relacionados ao assunto do artigo.
- Jamais faça um comentário com linguagem ofensiva ou de baixo calão, que deprecie o artigo exposto ou que ofenda o autor ou algum leitor do blog.
- Não coloque links de sites ou blogs no corpo do texto do comentário. Para isso, assine com seu Nome/URL ou OpenID.
-Não coloque seu email e nem seu telefone no corpo do texto do comentário. Use o nosso formulário de contato.
- Se encontrar algum pequeno erro na postagem, por favor, seja bem claro no comentário, pois a minha bola de cristal não é muito boa.
- Tem vezes que eu demoro pra responder, mas quase sempre eu respondo.
- Não seja tímido, se você tem alguma duvida ou sabe de algo mais sobre o assunto abordado no artigo, comente e compartilhe conosco :)