As equações diferenciais ordinárias (ou EDOs) são equações que envolvem, de forma implícita, pelo menos uma derivada de y.
Exemplos de aplicação
$a)2y.y'=1$
Resolução:
$2y.y'=1\Rightarrow 2y\left( \frac{dy}{dx} \right)=1\Rightarrow 2y.dy=1.dx\Rightarrow $
Aplicando a integral:
$\Rightarrow \int{2y.dy}=\int{1.dx}\Rightarrow \frac{2{{y}^{2}}}{2}+C=x+C\Rightarrow $
$\Rightarrow {{y}^{2}}+C=x+C\Rightarrow {{y}^{2}}=x+C\Rightarrow $
$\Rightarrow y=\pm \sqrt{x+C}$
$b)y=-\sqrt{x+7}$
Derivando em y:
$y=-\sqrt{x+7}\Rightarrow y'=\frac{-1}{2\sqrt{x+7}}\Rightarrow $
Substituindo y:
$\Rightarrow y'=\frac{1}{2y}\Rightarrow 2y.y'=1$
$c)\left( {{x}^{2}}+3 \right)dy-2xydx=0$
$\left( {{x}^{2}}+3 \right)dy-2xydx=0\Rightarrow \left( {{x}^{2}}+3 \right)dy=2xydx\Rightarrow $
$\Rightarrow \left( {{x}^{2}}+3 \right)\frac{dy}{dx}=2xy\Rightarrow \left( {{x}^{2}}+3 \right).y'=2xy\Rightarrow $
$\Rightarrow y'=\frac{2xy}{\left( {{x}^{2}}+3 \right)}\Rightarrow \frac{1}{y}.\frac{dy}{dx}=\frac{2x}{\left( {{x}^{2}}+3 \right)}\Rightarrow \frac{1}{y}.dy=\frac{2x}{\left( {{x}^{2}}+3 \right)}.dx\Rightarrow $
Integrando os dois lados: (Caso tenha dificuldade em fazer integral por substituição sugiro que você veja nosso post sobre esse assunto.)
$\Rightarrow \int{\frac{1}{y}dy}=\int{\frac{2x}{\left( {{x}^{2}}+3 \right)}dx}\Rightarrow \ln \left( y \right)=\ln \left( {{x}^{2}}+3 \right)+C\Rightarrow $
Aplicando logaritmos naturais:
$\Rightarrow {{e}^{\ln \left( y \right)}}={{e}^{\ln \left( {{x}^{2}}+3 \right)+C}}\Rightarrow {{e}^{\ln \left( y \right)}}={{e}^{\ln \left( {{x}^{2}}+3 \right)}}.{{e}^{C}}\Rightarrow y=\left( {{x}^{2}}+3 \right).{{e}^{C}}$
Como o logaritmo natural de C é ele mesmo, logo:
$y=\left( {{x}^{2}}+3 \right).C$
$d)\left( {{x}^{2}}+1 \right)dy+{{y}^{2}}dx=0$
$\left( {{x}^{2}}+1 \right)dy+{{y}^{2}}dx=0\Rightarrow \left( {{x}^{2}}+1 \right)dy=-{{y}^{2}}dx\Rightarrow $
$\Rightarrow -\frac{1}{{{y}^{2}}}dy=\frac{1}{\left( {{x}^{2}}+1 \right)}dx\Rightarrow $
Integrando os dois lados: (Caso necessário, consulte a nossa tabela de integrais elementares)
$\Rightarrow -\int{\frac{1}{{{y}^{2}}}dy}=\int{\frac{1}{\left( {{x}^{2}}+1 \right)}dx}\Rightarrow -\frac{1}{y}=arctg\left( x \right)+C\Rightarrow $
$\Rightarrow y=-\frac{1}{\left( arctg\left( x \right)+C \right)}$
$e)y'-y=0$
$y'-y=0\Rightarrow \frac{dy}{dx}-y=0\Rightarrow \frac{dy}{dx}=y\Rightarrow $
$\Rightarrow \frac{1}{y}dy=dx\Rightarrow $
Integrando os dois lados
$\Rightarrow \int{\frac{1}{y}dy}=\int{dx}\Rightarrow \ln \left( y \right)=x+C\Rightarrow $
$\Rightarrow y={{e}^{x+C}}$
Equações Diferenciais Ordinárias Lineares de Segunda Ordem Homogênea com Coeficientes Constantes
Essa EDOs são equações do tipo: y''+by'+cy = 0, em que b e c são constantes, sendo que a sua equação característica pode ser montada a partir da seguinte técnica:
Resolvendo a equação característica:
Então:
$y={{e}^{\alpha x}}\left( C1.\cos \left( \beta x \right)+C2.sen\left( \beta x \right) \right)$
$y={{e}^{\alpha x}}\left( C1.\cos \left( \beta x \right)+C2.sen\left( \beta x \right) \right)$
Exemplos de aplicação
Observação: Caso você não se lembre das regras de derivadas, veja o nosso post sobre regras de derivação.
a) y''-5y'+6y = 0 com y (0) = 10 e y’(0) = 26
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}-5r+6=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( -{{5}^{2}} \right)-4.\left( 1 \right).\left( 6 \right)=1$
$r1=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( -5 \right)-\sqrt{1}}{2}=2$
$r2=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( -5 \right)+\sqrt{1}}{2}=3$
$y\left( 0 \right)=10$
$y=C1.{{e}^{2x}}+C2.{{e}^{3x}}\Rightarrow 10=C1.{{e}^{2\left( 0 \right)}}+C2.{{e}^{3\left( 0 \right)}}\Rightarrow C1+C2=10$
$y'\left( 0 \right)=26$
$y'=C1.{{e}^{2x}}.2+C2.{{e}^{3x}}.3\Rightarrow 26=C1.{{e}^{2\left( 0 \right)}}.2+C2.{{e}^{3\left( 0 \right)}}.3\Rightarrow 2C1+3C2=26$
Logo,
$C1+C2=10\Rightarrow C1=10-C2~~\left( eq1 \right)$
$2C1+3C2=26~\left( eq2 \right)$
Substituindo a “eq1” na “eq2”:
$2C1+3C2=26~\Rightarrow 2\left( 10-C2 \right)+3C2=26~\Rightarrow $
$\Rightarrow 2\left( 10-C2 \right)+3C2=26~\Rightarrow 20-2C2+3C2=26\Rightarrow C2=6$
Logo:
$C1=10-6~~=4$
$y=C1.{{e}^{r1.x}}+C2.{{e}^{r2.x}}\Rightarrow y=4.{{e}^{2x}}+6.{{e}^{3x}}$
b) y''-10y'+25y = 0 com y(0)=3 e y'(0)=13
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}-10r+25=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( -{{10}^{2}} \right)-4.\left( 1 \right).\left( 25 \right)=0$
$r1=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( -10 \right)-\sqrt{0}}{2}=5$
$r2=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( -10 \right)+\sqrt{0}}{2}=5$
$y\left( 0 \right)=3$
$y=C1.{{e}^{5x}}+C2.x.{{e}^{5x}}\Rightarrow 3=C1.{{e}^{5\left( 0 \right)}}+C2.0.{{e}^{5\left( 0 \right)}}\Rightarrow C1=3$
$y'\left( 0 \right)=13$
$y'=C1.{{e}^{5x}}.5+C2.{{e}^{5x}}+C2.x.{{e}^{5x}}.5\Rightarrow $
$\Rightarrow 13=C1.{{e}^{5\left( 0 \right)}}.5+C2.{{e}^{5\left( 0 \right)}}+C2.0.{{e}^{5\left( 0 \right)}}.5\Rightarrow $
Substituindo o valor de C1:
$\Rightarrow 13=5C1+C2\Rightarrow 13=5\left( 3 \right)+C2\Rightarrow C2=-2$
Resposta:
$y=C1.{{e}^{5.x}}+C2.x{{e}^{5x}}\Rightarrow y=3.{{e}^{5x}}-2.{{e}^{5x}}$
c)y'' - 4y' +29y = 0 , com y(0) = 3 e y '(0) = 26
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}-4r+29=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( -{{4}^{2}} \right)-4.\left( 1 \right).\left( 29 \right)=-100$
$r1=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( -4 \right)-\sqrt{-100}}{2}=2-5i$
$r2=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( -10 \right)+\sqrt{-100}}{2}=2+5i$
$y\left( 0 \right)=3$
$y={{e}^{\alpha x}}\left( C1.\cos \left( \beta x \right)+C2.sen\left( \beta x \right) \right)$
Sendo α=2 e β=5, logo:
$y={{e}^{2x}}\left( C1.\cos \left( 5x \right)+C2.sen\left( 5x \right) \right)\Rightarrow 3={{e}^{2\left( 0 \right)}}\left( C1.\cos \left( 5\left( 0 \right) \right)+C2.sen\left( 5\left( 0 \right) \right) \right)\Rightarrow $
$\Rightarrow 3=1\left( C1.+0 \right)\Rightarrow C1=3$
$y'\left( 0 \right)=26$
$y'={{e}^{2x}}.2.\left( C1.\cos \left( 5x \right)+C2.sen\left( 5x \right) \right)+{{e}^{2x}}\left( C1.-sen\left( 5x \right).5+C2.\cos \left( 5x \right).5 \right)\Rightarrow $
$\Rightarrow 26={{e}^{2\left( 0 \right)}}.2.\left( C1.\cos \left( 0 \right)+C2.sen\left( 0 \right) \right)+{{e}^{2\left( 0 \right)}}\left( C1.-sen\left( 0 \right).5+C2.\cos \left( 0 \right).5 \right)\Rightarrow $
$\Rightarrow 26=2.\left( C1 \right)+\left( 5C2 \right)\Rightarrow $
Substituindo o valor de C1:
$\Rightarrow 26=2.\left( 3 \right)+\left( 5C2 \right)\Rightarrow 26=6+5C2\Rightarrow 5C2=20\Rightarrow C2=4$
Resposta:
$y={{e}^{2x}}\left( 3.\cos \left( 5x \right)+4.sen\left( 5x \right) \right)$
d) y'' +3y' =0 com y(0) =9 e y'(0) = -6
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}+3r+=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( {{3}^{2}} \right)-4.\left( 1 \right).\left( 0 \right)=9$
$r1=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( 3 \right)+\sqrt{9}}{2}=0$
$r2=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( 3 \right)-\sqrt{9}}{2}=-3$
$y\left( 0 \right)=9$
$y=C1.{{e}^{0.x}}+C2.{{e}^{-3x}}\Rightarrow y=C1+C2.{{e}^{-3x}}\Rightarrow $
$\Rightarrow 9=C1+C2.{{e}^{-3\left( 0 \right)}}\Rightarrow C1=9-C2$
$y'\left( 0 \right)=-6$
$\Rightarrow y'=-3.C2.{{e}^{-3x}}\Rightarrow -6=-3.C2.{{e}^{-3\left( 0 \right)}}\Rightarrow $
$\Rightarrow 6=3.C2\Rightarrow C2=2$
Logo:
$\Rightarrow C1=9-2=7$
Resposta:
$y=7.{{e}^{0.x}}+C2.{{e}^{-3x}}\Rightarrow y=7+2{{e}^{-3x}}$
a) y''-5y'+6y = 0 com y (0) = 10 e y’(0) = 26
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}-5r+6=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( -{{5}^{2}} \right)-4.\left( 1 \right).\left( 6 \right)=1$
$r1=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( -5 \right)-\sqrt{1}}{2}=2$
$r2=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( -5 \right)+\sqrt{1}}{2}=3$
$y\left( 0 \right)=10$
$y=C1.{{e}^{2x}}+C2.{{e}^{3x}}\Rightarrow 10=C1.{{e}^{2\left( 0 \right)}}+C2.{{e}^{3\left( 0 \right)}}\Rightarrow C1+C2=10$
$y'\left( 0 \right)=26$
$y'=C1.{{e}^{2x}}.2+C2.{{e}^{3x}}.3\Rightarrow 26=C1.{{e}^{2\left( 0 \right)}}.2+C2.{{e}^{3\left( 0 \right)}}.3\Rightarrow 2C1+3C2=26$
Logo,
$C1+C2=10\Rightarrow C1=10-C2~~\left( eq1 \right)$
$2C1+3C2=26~\left( eq2 \right)$
Substituindo a “eq1” na “eq2”:
$2C1+3C2=26~\Rightarrow 2\left( 10-C2 \right)+3C2=26~\Rightarrow $
$\Rightarrow 2\left( 10-C2 \right)+3C2=26~\Rightarrow 20-2C2+3C2=26\Rightarrow C2=6$
Logo:
$C1=10-6~~=4$
$y=C1.{{e}^{r1.x}}+C2.{{e}^{r2.x}}\Rightarrow y=4.{{e}^{2x}}+6.{{e}^{3x}}$
b) y''-10y'+25y = 0 com y(0)=3 e y'(0)=13
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}-10r+25=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( -{{10}^{2}} \right)-4.\left( 1 \right).\left( 25 \right)=0$
$r1=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( -10 \right)-\sqrt{0}}{2}=5$
$r2=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( -10 \right)+\sqrt{0}}{2}=5$
$y\left( 0 \right)=3$
$y=C1.{{e}^{5x}}+C2.x.{{e}^{5x}}\Rightarrow 3=C1.{{e}^{5\left( 0 \right)}}+C2.0.{{e}^{5\left( 0 \right)}}\Rightarrow C1=3$
$y'\left( 0 \right)=13$
$y'=C1.{{e}^{5x}}.5+C2.{{e}^{5x}}+C2.x.{{e}^{5x}}.5\Rightarrow $
$\Rightarrow 13=C1.{{e}^{5\left( 0 \right)}}.5+C2.{{e}^{5\left( 0 \right)}}+C2.0.{{e}^{5\left( 0 \right)}}.5\Rightarrow $
Substituindo o valor de C1:
$\Rightarrow 13=5C1+C2\Rightarrow 13=5\left( 3 \right)+C2\Rightarrow C2=-2$
Resposta:
$y=C1.{{e}^{5.x}}+C2.x{{e}^{5x}}\Rightarrow y=3.{{e}^{5x}}-2.{{e}^{5x}}$
c)y'' - 4y' +29y = 0 , com y(0) = 3 e y '(0) = 26
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}-4r+29=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( -{{4}^{2}} \right)-4.\left( 1 \right).\left( 29 \right)=-100$
$r1=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( -4 \right)-\sqrt{-100}}{2}=2-5i$
$r2=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( -10 \right)+\sqrt{-100}}{2}=2+5i$
$y\left( 0 \right)=3$
$y={{e}^{\alpha x}}\left( C1.\cos \left( \beta x \right)+C2.sen\left( \beta x \right) \right)$
Sendo α=2 e β=5, logo:
$y={{e}^{2x}}\left( C1.\cos \left( 5x \right)+C2.sen\left( 5x \right) \right)\Rightarrow 3={{e}^{2\left( 0 \right)}}\left( C1.\cos \left( 5\left( 0 \right) \right)+C2.sen\left( 5\left( 0 \right) \right) \right)\Rightarrow $
$\Rightarrow 3=1\left( C1.+0 \right)\Rightarrow C1=3$
$y'\left( 0 \right)=26$
$y'={{e}^{2x}}.2.\left( C1.\cos \left( 5x \right)+C2.sen\left( 5x \right) \right)+{{e}^{2x}}\left( C1.-sen\left( 5x \right).5+C2.\cos \left( 5x \right).5 \right)\Rightarrow $
$\Rightarrow 26={{e}^{2\left( 0 \right)}}.2.\left( C1.\cos \left( 0 \right)+C2.sen\left( 0 \right) \right)+{{e}^{2\left( 0 \right)}}\left( C1.-sen\left( 0 \right).5+C2.\cos \left( 0 \right).5 \right)\Rightarrow $
$\Rightarrow 26=2.\left( C1 \right)+\left( 5C2 \right)\Rightarrow $
Substituindo o valor de C1:
$\Rightarrow 26=2.\left( 3 \right)+\left( 5C2 \right)\Rightarrow 26=6+5C2\Rightarrow 5C2=20\Rightarrow C2=4$
Resposta:
$y={{e}^{2x}}\left( 3.\cos \left( 5x \right)+4.sen\left( 5x \right) \right)$
d) y'' +3y' =0 com y(0) =9 e y'(0) = -6
Resolução:
$Eq.caracter\acute{i}stica:{{r}^{2}}+3r+=0\Rightarrow $
$\Rightarrow \Delta =\left( {{b}^{2}} \right)-4.a.c\Rightarrow \Delta =\left( {{3}^{2}} \right)-4.\left( 1 \right).\left( 0 \right)=9$
$r1=\frac{-b+\sqrt{\Delta }}{2a}\Rightarrow r2=\frac{-\left( 3 \right)+\sqrt{9}}{2}=0$
$r2=\frac{-b-\sqrt{\Delta }}{2a}\Rightarrow r1=\frac{-\left( 3 \right)-\sqrt{9}}{2}=-3$
$y\left( 0 \right)=9$
$y=C1.{{e}^{0.x}}+C2.{{e}^{-3x}}\Rightarrow y=C1+C2.{{e}^{-3x}}\Rightarrow $
$\Rightarrow 9=C1+C2.{{e}^{-3\left( 0 \right)}}\Rightarrow C1=9-C2$
$y'\left( 0 \right)=-6$
$\Rightarrow y'=-3.C2.{{e}^{-3x}}\Rightarrow -6=-3.C2.{{e}^{-3\left( 0 \right)}}\Rightarrow $
$\Rightarrow 6=3.C2\Rightarrow C2=2$
Logo:
$\Rightarrow C1=9-2=7$
Resposta:
$y=7.{{e}^{0.x}}+C2.{{e}^{-3x}}\Rightarrow y=7+2{{e}^{-3x}}$
Referências
- Notas de Cálculo Integral e Diferencial, Profº Sergio, Unisanta, Santos, São Paulo, 2011.
- Notas de Cálculo Integral e Diferencial, Pedro Coelho, Santos, São Paulo, 2011.
Sobre o autor
 Olá meu nome é Pedro Coelho, eu sou engenheiro químico, engenheiro de segurança do trabalho e Green Belt em Lean
Six Sigma. Além disso, também sou estudante de engenharia civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)
Olá meu nome é Pedro Coelho, eu sou engenheiro químico, engenheiro de segurança do trabalho e Green Belt em Lean
Six Sigma. Além disso, também sou estudante de engenharia civil, e em parte de minhas horas vagas me dedico a escrever artigos aqui no ENGQUIMICASANTOSSP, para ajudar estudantes de Engenharia Química e de áreas correlatas. Se você está curtindo essa postagem, siga-nos através de nossas paginas nas redes sociais e compartilhe com seus amigos para eles curtirem também :)
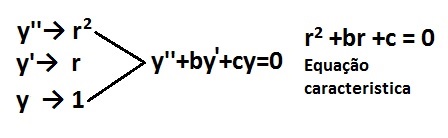
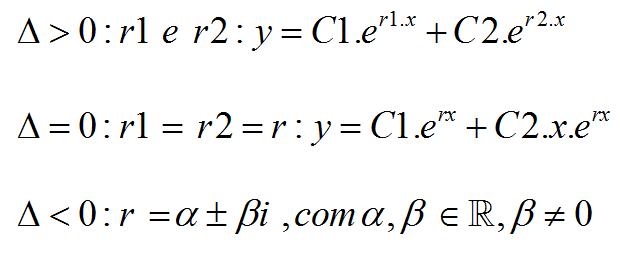

1 Comentários de "Equações Diferenciais Ordinárias (EDO): Exemplos de aplicação"
Parabéns pelo seu trabalho.
Os comentários são sempre bem vindos, pois agregam valor ao artigo. Porém, existem algumas regras na Política de Comentários, que devem ser seguidas para o seu comentário não ser excluído:
- Os comentários devem estar relacionados ao assunto do artigo.
- Jamais faça um comentário com linguagem ofensiva ou de baixo calão, que deprecie o artigo exposto ou que ofenda o autor ou algum leitor do blog.
- Não coloque links de sites ou blogs no corpo do texto do comentário. Para isso, assine com seu Nome/URL ou OpenID.
-Não coloque seu email e nem seu telefone no corpo do texto do comentário. Use o nosso formulário de contato.
- Se encontrar algum pequeno erro na postagem, por favor, seja bem claro no comentário, pois a minha bola de cristal não é muito boa.
- Tem vezes que eu demoro pra responder, mas quase sempre eu respondo.
- Não seja tímido, se você tem alguma duvida ou sabe de algo mais sobre o assunto abordado no artigo, comente e compartilhe conosco :)